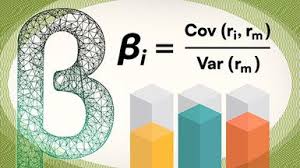
Understanding Beta in the CAPM Model

In finance, beta (β) is a cornerstone concept within the Capital Asset Pricing Model (CAPM) that quantifies an asset’s sensitivity to systematic risk—the risk inherent to the entire market. It measures how much a security’s returns tend to move relative to market fluctuations, helping investors assess risk-adjusted expected returns.

What is Beta?

Beta is calculated as:

β = Cov (Ri,Rm) / Var(Rm)

where:

• Ri = Return of the asset
• Rm = Return of the market
• Cov = Covariance between the asset and market returns
• Var = Variance of the market returns

This formula shows beta as a statistical measure of volatility relative to a benchmark.

Interpreting Beta Values

• β = 1: The asset moves in lockstep with the market (average systematic risk).
• β > 1: The asset is more volatile than the market (e.g., β = 1.5 implies 50% more volatility).
• β < 1: The asset is less volatile than the market (e.g., β = 0.8 implies 20% less volatility).
• β < 0: The asset moves inversely to the market (rare, but seen in assets like gold or certain defensive stocks).

Beta’s Role in the CAPM

The CAPM formula links beta to expected returns:

E(Ri) = Rf + βi (E (Rm) − Rf)

• E(Ri) = Expected return of the asset
• Rf = Risk-free rate (e.g., government bonds)
• E(Rm)−Rf = Market risk premium

Key insights:

Higher beta = Higher expected return (compensation for greater risk).

Lower beta = Lower expected return (safer, but with reduced upside).

The market itself has a beta of 1.0 by definition.

Practical Applications

Portfolio Construction:

• Combine high-beta stocks (for growth) with low-beta stocks (for stability) to balance risk.
• A portfolio’s beta is the weighted average of its constituents’ betas.

Valuation:

• Used to calculate a company’s cost of equity.
• For example, a stock with β = 1.2, Rf=4% , and a market risk premium of 5% would have a cost of equity of 4%+1.2×5%=10%.

Limitations:

• Assumes markets are efficient and returns follow a normal distribution—criticized for oversimplifying real-world dynamics.
• Does not account for asymmetric risk (e.g., frequent downside shocks).

Example

Suppose a stock has:

• Correlation with the market (ρimρim) = 0.80
• Standard deviation of stock returns (σiσi) = 40%
• Standard deviation of market returns (σmσm) = 20%

Beta is calculated as:

β = 0.80×0.40/0.20 = 1.6

This stock is 60% more volatile than the market.

Why Beta Matters

Beta provides a standardized way to gauge risk and align investments with risk tolerance. While imperfect, it remains a foundational tool in modern portfolio theory and corporate finance.

For investors, understanding beta means better decisions about balancing risk and reward in pursuit of financial goals.